(Why it matters, how to calculate it, and where it’s used – made simple)
In reinforced concrete design, development length plays a crucial role in ensuring that steel reinforcement can effectively transfer stress to the surrounding concrete. It’s one of those technical terms you must understand deeply if you’re a civil engineering student, site engineer, or design professional.
What is Development Length?
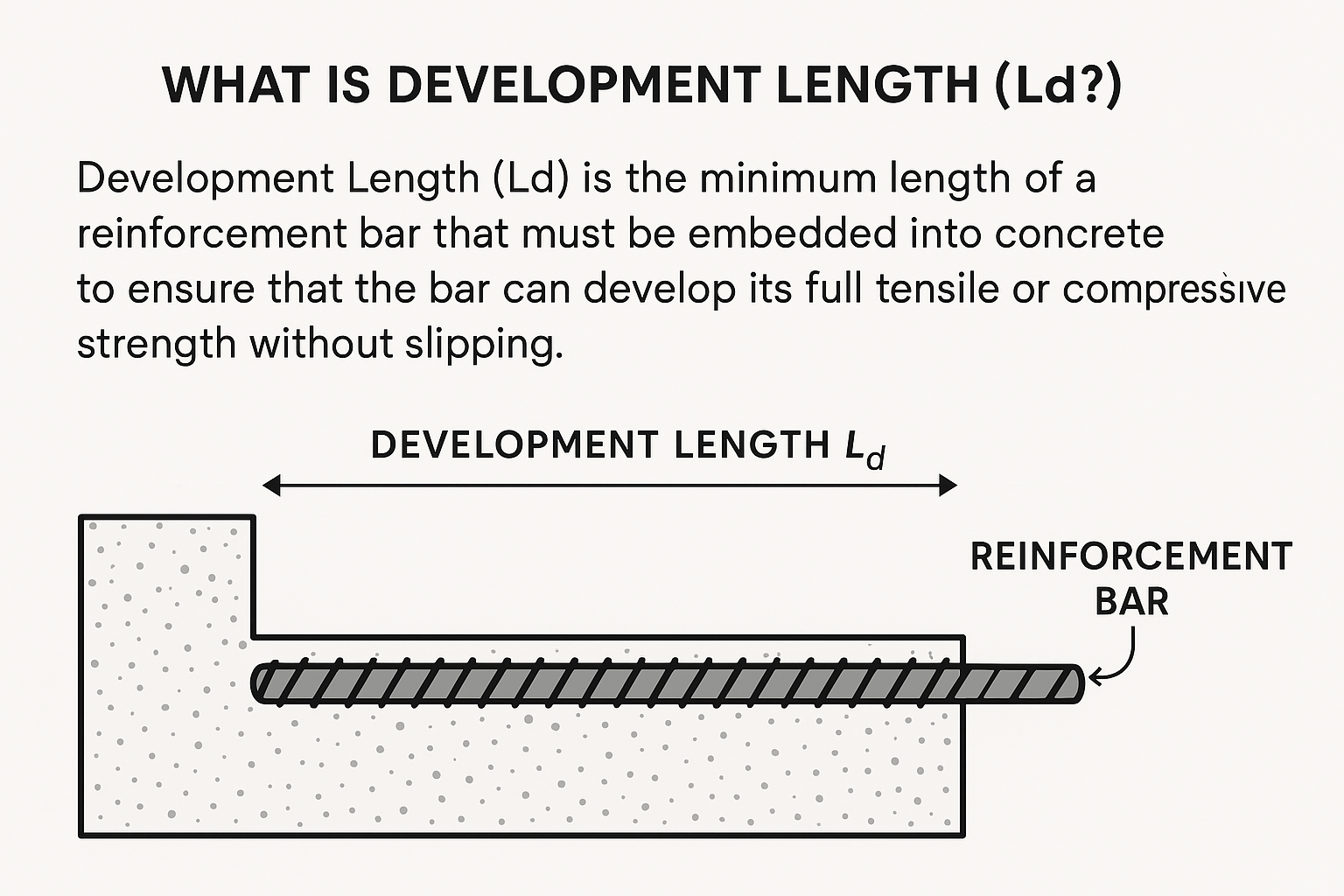
Development length (denoted as Ld) is the minimum length of a reinforcing bar that must be embedded or anchored in concrete to ensure the full strength of the bar is developed before it starts to slip.
This means it allows steel to “grip” into concrete without failing or pulling out, especially in tension or compression zones.
IS 456:2000 Definition (Clause 26.2.1):
“The development length is the length of the bar required to develop the full strength of the reinforcement at a critical section.”

You can download IS 456:2000 and other essential IS codes here — all compiled in one place for quick reference.
Why is Development Length So Important?
- It prevents bond failure between steel and concrete
- It ensures safe load transfer under tension and compression
- Critical in beam-column joints, footings, slabs, and splicing zones
- It helps structures resist seismic and wind loads by maintaining integrity
Development Length Formula (As Per IS 456:2000)
Ld=Φ×σs4×τbd\boxed{Ld = \frac{Φ \times σ_s}{4 \times τ_{bd}}}Ld=4×τbdΦ×σsWhere:
- Ld = Development Length (mm)
- Φ = Diameter of the bar (mm)
- σs = Stress in steel (typically 0.87 × fy)
- τbd = Design bond stress (N/mm²)
- fy = Yield strength of steel (usually 415 or 500 MPa)
Bond Stress (τbd) from IS 456:2000 Table 21
The value of design bond stress (τbd) depends on the type of bar and concrete grade:
| Concrete Grade | τbd for Plain Bars (N/mm²) | τbd for Deformed Bars (↑ 60%) |
|---|---|---|
| M20 | 1.2 | 1.92 |
| M25 | 1.4 | 2.24 |
| M30 | 1.5 | 2.40 |
✔️ For compression bars, τbd is increased by 25%
✔️ For good bond conditions, standard values apply
✔️ For poor bond conditions, reduce τbd by 25%
Practical Example:
Let’s calculate Ld for a Fe 500 steel bar with 16 mm diameter in M25 concrete (good bond conditions):
- Φ = 16 mm
- fy = 500 MPa
- σs = 0.87 × 500 = 435 MPa
- τbd (M25, deformed) = 2.24 N/mm²
L_d = \frac{4 \times \tau_s}{\phi \times \sigma_s} = \frac{4 \times 2.24}{16 \times 435} = \frac{8.96}{6960} \approx 0.00129\, \text{m} \approx 777\, \text{mm}
You must provide at least 777 mm anchorage for that bar in tension.
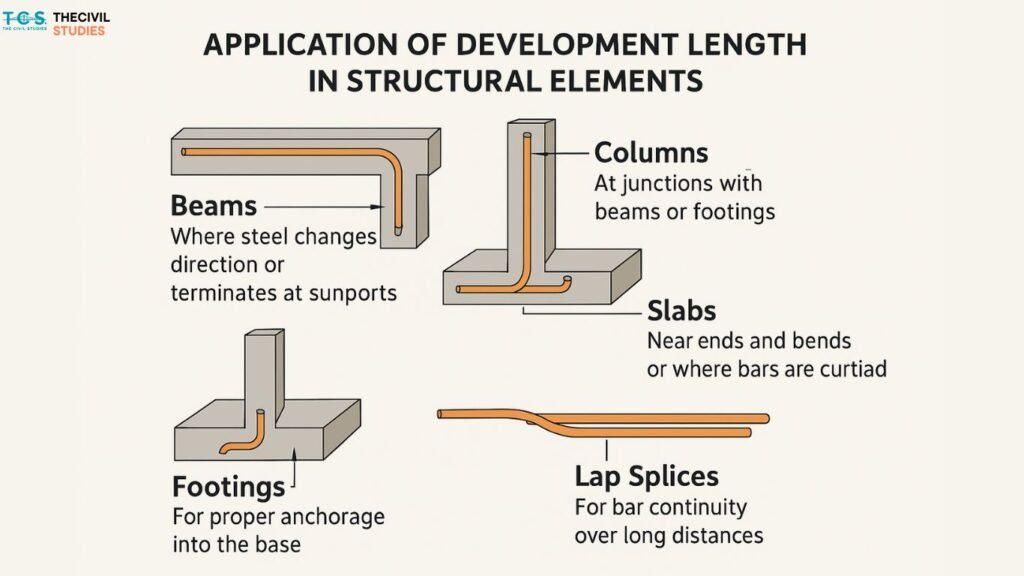
Application of Development Length in Structural Elements
Here’s how development length comes into play in various structural parts:
- Beams: Where steel changes direction or terminates at supports
- Columns: At junctions with beams or footings
- Slabs: Near ends and bends or where bars are curtailed
- Footings: For proper anchorage into the base
- Lap Splices: For bar continuity over long distances
Techniques to Reduce Required Length
Sometimes space is limited, so engineers use additional anchorage:
- Hooks (for tension zones)
- Bends at bar ends
- Mechanical couplers
- Welded joints
Key IS Code References
- IS 456:2000 – Clause 26.2 (Development Length)
- SP 34 – Detailing of reinforcement
- IS 13920 (for seismic detailing)
Quick Summary
- Development length ensures safe load transfer between steel and concrete.
- Calculated using Ld = (Φ × σs)/(4 × τbd).
- Depends on bar diameter, bond stress, and steel grade.
- Use hooks, bends, or couplers if full length is not available.
- Mandatory in structural joints, footings, and splicing zones.





[…] is fundamental to structural integrity. Two terms that are often misused or misunderstood—development length and anchorage length—serve unique and critical purposes in load transfer and durability of RCC […]